Quaternion Class Reference

Quaternions are an extension of real numbers used to represent rotations in 3D. More...

#include <DualQuaternion.hpp>

Public Member Functions
	Quaternion ()=default
	Quaternion (float x, float y, float z, float w)
template<typename Q , typename std::enable_if< not std::is_floating_point< Q >::value >::type * = nullptr>
	Quaternion (const Q &q)
template<typename F , typename std::enable_if< std::is_floating_point< F >::value >::type * = nullptr>
	Quaternion (F f)
template<typename V3 >
	Quaternion (const V3 &unitAxis, float thetaRadians)
	Constructs a unit quaternion from the specified unit 3D vector and rotation angle. More...

Static Public Member Functions
static const Quaternion	identity ()
template<typename V3 >
static const V3	toVector (const Quaternion &q)
template<typename V3 >
static const Quaternion	fromVector (const V3 &v)
	Constructs a quaternion by embedding (identifying with) a 3D vector. More...
template<typename M3 >
static const M3	toMatrix (const Quaternion &q)
template<typename M3 >
static const Quaternion	fromMatrix (const M3 &m)

Public Attributes
float	x
float	y
float	z
	Vector part of the quaternion. More...
float	w
	Scalar part of the quaternion. More...

Detailed Description

Quaternions are an extension of real numbers used to represent rotations in 3D.

Quaternions are an alternative to Euler angles or rotation matrices (and others). They don't have singularities (Euler angles' gimbal lock), they are more compact than matrices (4 floats) and can be extended to represent translations as well (dual quaternions). As a set, the quaternions form 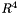, four-dimensional vector space over the real numbers (meaning they possess the usual addition and scalar multiplication). In addition, quaternions can also be multiplied. Multiplication is associative, but (unlike multiplication of real or complex numbers) it is not commutative. There are many resources out there available covering quaternions much more extensively. This particular implementation is a very minimal one: a constructor taking 3D unit vector (axis of rotation) and rotation angle, addition and multiplication operators, methods converting to/from 3x3 matrices and a conjugate function (non-member). Example usage can be found in DualQuaternionTests.cpp file.

Constructor & Destructor Documentation

Quaternion::Quaternion ( )

default

Quaternion::Quaternion ( float  x, float  y, float  z, float  w  )

inline

template<typename Q , typename std::enable_if< not std::is_floating_point< Q >::value >::type * = nullptr>

Quaternion::Quaternion ( const Q &  q )

inline

This constructor is enabled only when Q is not a float (assuming Q will then be a different implementation of quaternions). Q must have public x,y,z,w members.

template<typename F , typename std::enable_if< std::is_floating_point< F >::value >::type * = nullptr>

Quaternion::Quaternion ( F  f )

inline

Constructor enabled when F is a floating point. Constructs (0,0,0,f). Real numbers are a subset of quaternions (when x, y and z are zero). For example 2.f * Quaternion() is actually implemented as Quaternion(2.f) * Quaternion().

template<typename V3 >

Quaternion::Quaternion ( const V3 &  unitAxis, float  thetaRadians  )

inline

Constructs a unit quaternion from the specified unit 3D vector and rotation angle.

Member Function Documentation

template<typename M3 >

static const Quaternion Quaternion::fromMatrix ( const M3 &  m )

inlinestatic

Converts a pure rotation (orthogonal) 3x3 matrix to unit quaternion. Templatized on matrix type (requires an operator() (row, column)). For more information, see e.g. Real-Time Rendering (Haines, Hoffman, Akenine-Möller).

template<typename V3 >

static const Quaternion Quaternion::fromVector ( const V3 &  v )

inlinestatic

Constructs a quaternion by embedding (identifying with) a 3D vector.

static const Quaternion Quaternion::identity ( )

inlinestatic

Constructs a unit quaternion representing no rotation (vector component is 0, scalar is set to 1).

template<typename M3 >

static const M3 Quaternion::toMatrix ( const Quaternion &  q )

inlinestatic

Converts a quaternion to 3x3 rotation matrix. Assumes quaternion q is unit (rotation only). Templatized on matrix type (requires an operator() (row, column)).

template<typename V3 >

static const V3 Quaternion::toVector ( const Quaternion &  q )

inlinestatic

Returns the vector embedded in a quaternion. Templatized to support various different implementations of 3D vectors. Example usage: Quaternion::toVector<nv::vec3f>(q).

Member Data Documentation

float Quaternion::w

Scalar part of the quaternion.

float Quaternion::x

float Quaternion::y

float Quaternion::z

Vector part of the quaternion.

---

The documentation for this class was generated from the following file:

• DualQuaternion.hpp